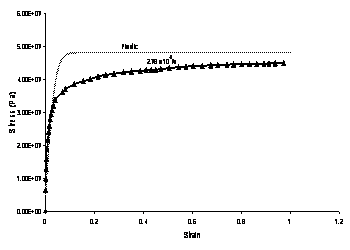
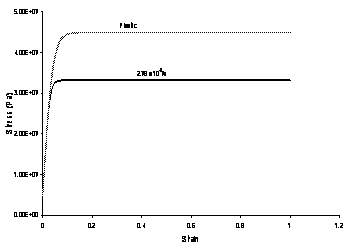
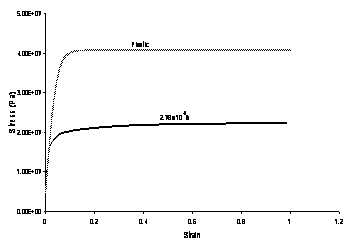
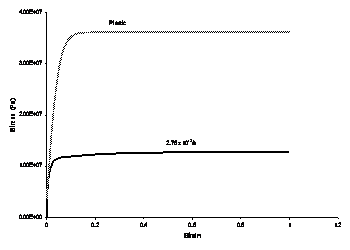
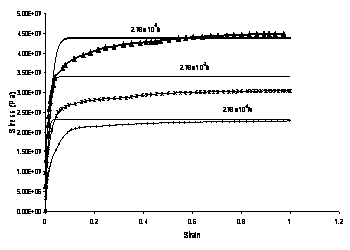
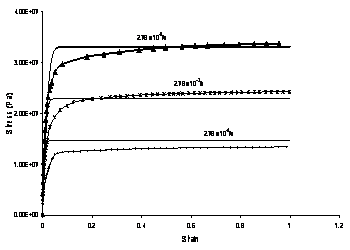
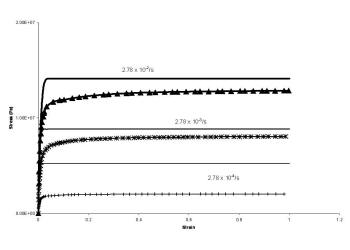
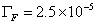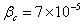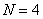Solder is an alloy of lead and tin, and averaged properties were determined to compute the number of atoms per unit volume at 0K, the packing fraction and the molar specific heat. Plastic yielding was modeled by assuming the highest strain rate curve at the lowest temperature available to be close to the true plasticity curve. Thus, unlike the simplified rate-dependent simulations or the Perzyna viscoplastic solder simulations, the thermomechanical model incorporates plastic and creep strains separately.

For the elastic part of the thermomechanical model, for consistency of procedure in the code, the number of particles per unit volume was computed by assigning an average weight to the atoms to get an equivalent atomic weight. This is simply an intermediate step in the procedure, and thus, not relevant to the results. The atomic weight was assigned based on the computation that the number of atoms in eutectic solder is approximately 24% Lead and 76% Tin. Similarly, an average bonding energy was assigned to the atoms. The actual value of the bonding energy is not critical as it is used in conjunction with the empirical scale factor h. Finally, since at 0K both Lead and Tin are in the fcc state, a packing fraction of 0.74 was maintained for solder.

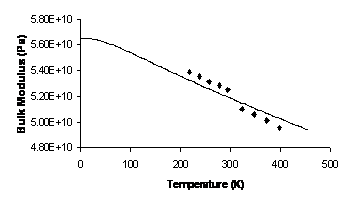
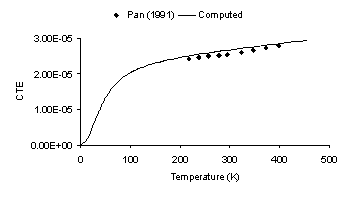
Experimental values of the Young’s modulus, E, and Poisson’s Ratio, n, have been provided for certain values of the temperature by Pan (1991) from which observed values of bulk modulus and the shear modulus may be obtained.

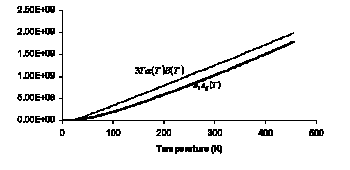
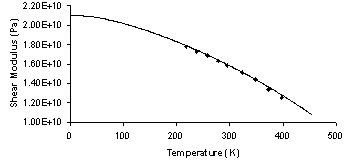
For estimating the 0K value of the bulk modulus, B₀, along with the empirical scale factor h, predictions for the variation of both the coefficient of thermal expansion and bulk modulus with temperature were curve-fit simultaneously. No formal optimization was required as the variation of material parameters with temperature is quite systematic with the parameters B₀ and h. Similar to the case for Tin, the latent heat of fusion requires empirical modification for solder. The shear modulus at 0K, G₀ and the modified U^L were determined by obtaining the best fit values for the material parameters to the curve for the variation of shear modulus with temperature. For simplicity, the specific heat used was the weighted average value for Lead and Tin based on the Kopp Neumann rule which is frequently assumed to be valid for alloys, although it is intended for compounds (Reed and Clark, 1983).

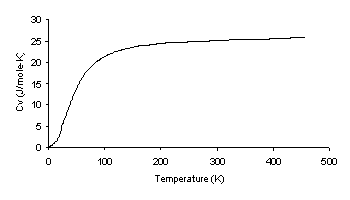
Molar Specific Heat Averaged from Lead and Tin

Results for solder show that based on averaged molar specific heat and two empirical scale factors for the bonding energy and energy required for liquefaction, as well as basic physical parameters, extremely reasonable predictions, including extrapolations are obtained for solder for the coefficient of thermal expansion as well as the elastic constants. This is helpful as elastic parameters are difficult to measure. The model does not have externally required temperature-dependence of material parameters, as is the case for other models where some empirical function is required to describe the temperature dependence. It is consistent with the the first law of thermodynamics by design and reasonably as seen from the results, with the second law, thereby implicitly satisfying the thermoelastic relationships. 

Coefficient of Thermal Expansion

Consistency with Second Law

Bulk Modulus

Shear Modulus

For plastic deformations, consistent with the assumption that approximately 10% of the dissipated plastic work is absorbed in the crystal, while the rest is dissipated as heat, it may be assumed that

Based on the modified U^L used for solder, the maximum shear stress that the material could withstand at –20^oC and high strain rates, ignoring creep, is approximately 150 MPa, while the maximum value obtained by Wang et al (2001) is approximately 45 MPa. Thus, assuming that creep does not play a large role at the highest strain‑rate curve available for the lowest temperature, we approximate

The rate‑independent elastoplastic curves for solder in the absence of creep for solder at various temperatures, along with the highest strain-rate test curves available show that as expected, the effect of creep increases with temperature, causing larger deviations from the elastoplastic behavior.

T = -20^oC

T = 25^oC

T = 75^oC

T = 125^oC

For creep, three additional parameters, G_F, N and b_c need to be determined for Eq. (5.73). These parameters were determined by manually fitting all the twelve curves from the data of Wang (2001) simultaneously. The values obtained were

Based on these values, the plots for all curves are obtained. It may be noted that unlike the elastoplastic simulation where each of the twelve available test curves require a different set of parameters, and Perzyna viscoplastic simulation where at each temperature a different set of parameters was required and the anomalous behavior of the flow parameter with temperature made interpolation as a function of temperature difficult, for the thermomechanical model only three additional temperature independent parameters are used to obtain creep behavior under the full range of temperature and strain rates. The issues with the fluidity parameter in Perzyna were predicted due to the limitations of ignoring plastic strains, which was anticipated to provide spurious values of the parameter at low temperatures.

T = -25^oC

T = 25^oC

T = 75^oC

T = 125^oC

Except for the highest temperature and the lowest strain rate, the creep equation provides extremely reasonable predictions with a minimal number of material parameters. The test curves it must be noted, are extrapolations from the test data assuming no damage. For the lowest strain rate test curve at the highest temperature, the damage due to creep is extremely high even at small strains, and it may be possible that the extrapolation was inordinately influenced to the lower side by the initial damage that was induced in the very initial stages of the test, making the prediction substantially higher than the test.