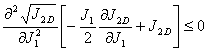The convexity
condition for yield functions in the
vs.
plane
has been assumed by Chen (1997) to be
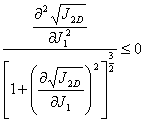
The sign may be reversed in literature depending on whether a convex curve is defined as convex up or convex down. However, this condition does not ensure that the point that defines the state of stress for a material always lies within the yield surface.
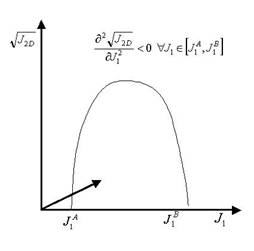
Thus, proof of satisfaction of the convexity condition above is not sufficient to demonstrate the validity of the yield surfaces. For instance, Chen (1997) showed numerically for HiSS-d0 function of Desai (2001) that the condition is always satisfied for HiSS-d0, if the parameter n > 2. A simple analytical proof is in Dube (2004), based on the fact that the denominator is always positive. The constraint n>2 is required to ensure that J2D is always positive as expected. However, several HiSS surfaces lie outside of the initial state of a material with zero plastic strain at zero stress (Dube, 2004).
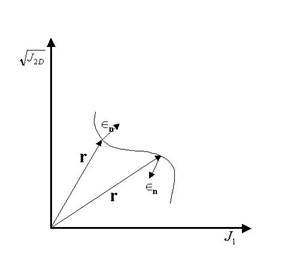
The convexity requirement can be satisfied along with the condition that the allowable states of stress for any hardening be within the yield surface corresponding to the given value of hardening, by noting that the origin is always within the yield surface as the material can be unloaded without further plastic deformation, and thus, requiring the dot product of the position vector to any point on the yield surface where J2D is not zero, with the curvature of the surface at that point to be negative (Dube, 2004).
For this condition, the required convexity condition
for a yield function defined in terms of
the invariants of stress in the
vs.
plane is
