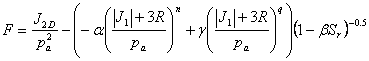Simple Solutions within HiSS

Due to the widespread use of HiSS over several decades, several simple solutions were proposed within the HiSS framework so as to mitigate certain specific issues. However, for comprehensive resolution of all issues, the new yield function is required.

Hardening Parameters

The existing procedure for computation of a1 and h1 (Desai, 2001) requires plotting ln(a) vs. ln(x). For computing x, only incremental values are obtained based on test data‑points, while computation of x₀ requires the parameters a1 and h1. Thus far, parameter determination has implicitly assumed x₀ to be zero. An iterative procedure was developed in Dube (2004) wherein parameters are first estimated assuming x₀ to be zero. Next x₀ is estimated based on the parameters. The parameters are then recomputed incorporating the x₀ estimate, and the procedure is continued till internally consistent values of a1, h1 and x₀ are obtained to within the desired accuracy.

Spurious Plastic Strains

The iterative parameter determination procedure does not correct the problem of discontinuous yield under tensile loads or spurious plastic strains under thermal loading. Li (2002), based on the iterative parameter determination procedure (Dube, 2004) has modified the hardening function as

Essentially, x₀, which is computed based on the plasticity parameters, is now taken simply to be a material parameter, say c, rather than a component of the plastic strain trajectory. This resolves the spurious thermal plastic strain issue as c takes up any change previously attributed to x through the temperature-dependent x₀. The iterative procedure for parameter determination is required to compute internally consistent values of a1, h1 and c.

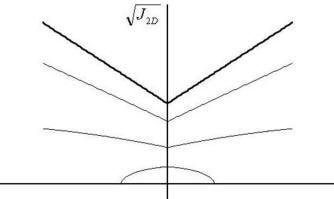
However, this again does not resolve discontinuous yield under tensile loads and lack of an initial elastic incremental stress‑strain matrix for compressive loading in the limit of zero stress.

Discontinuous Yield

For resolving discontinuous yield under tensile loads within the HiSS framework, Dube (2004) suggesting using |J₁| instead of J₁ in the yield function equation to provide

 

 

The problem with this function, as shown in the plot, is that the final failure stress also increases with increasing tensile mean pressure and the material never fails under hydrostatic tensile mean pressure. It also does not resolve the issue of the initial elastoplastic matrix at zero stress not being the elastic matrix.

 All of these issues are resolved in a comprehensive manner with the new yield function, which starts at the origin, inherently provides continuous yielding in both tension and compression, has a temperature‑independent value of zero for the plastic strain trajectory with no spurious thermally generated plastic strains, and provides an initial elastoplastic matrix that tends to the elastic matrix in the limit of zero stress.