Simplified Simulations

Two simplifications, the rate-dependent elastoplastic formulation and the Perzyna viscoplastic formulation, have been used for modeling plastic and creep strains under the HiSS/DSC scheme of Desai (2001). These are studied here with regard to the displacement-controlled, isothermal, unidirectional simple shear tests of Pb/Sn solder at constant strain‑rates of 2.78x10^-4, 2.78x10^-3, and 2.78x10^-2/s conducted by Wang et. al. (2001) at -20, 25, 75 and 125^oC.

Since yield function issues are relevant, both to the elastic formulation and the Perzyna viscoplastic formulation which has an elastoplastic static yield surface, these are discussed after the results from both formulations are described.

Rate-dependent Elastoplastic

The elastoplastic scheme assumes all inelastic strain to be instantaneous, rate‑independent plastic  deformation. The total strain increment is

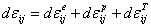
comprised of the elastic, e, plastic, p, and thermal, T, components. To incorporate rate‑dependence due to creep, material parameters are strain‑rate dependent (Chia, 1994;  Desai and Whitenack, 2001; Wang et al., 2001; Li, 2003)

The governing elastic incremental equation is the generalized equation developed here,

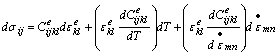
where assuming linear elasticity, C^e_ijkl is the secant history‑independent, strain‑rate and temperature dependent elastic constitutive matrix.

As shown, this leads to stress discontinuity at points of loading where the strain rate changes abruptly, indicating that the scheme is not appropriate for solder modeling except for constant strain rate tests. Since testing and parameter determination are useful only in that results can be translated to field conditions, the scheme is simply a theoretical exercise, which nonetheless provides some useful information regarding the yield function issues.

Parameter Determination

Parameters are presented for the new yield function, for the HiSS-d₀ function with hardening parameters based on the procedure of Desai (2001) and for the HiSS-d₀ function based on the iterative parameter scheme developed here for the hardening parameters. Details are in Dube (2004).

Solder Parameters for Elastoplastic Scheme

n = 0.4; g = 0.00112; b = 0; n (HiSS) = 2.15 (Wang et al., 2001); n (new function) = 2

Note that the value of R provided by Wang et al. (2001) is substantially higher than the value computed here based on the fundamental relationship between R, the parameter g, and the ultimate shear stress for shear loading under zero confining pressure, t_ult,

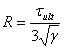
This is significant since the elastoplastic scheme is of limited utility and the corrected parameters permit use of the more appropriate Perzyna formulation, which was not feasible based on the value of R presented by Wang et al., (2001).

The iterative parameter determination scheme provides internally consistent values of the hardening parameters and the plastic strain trajectory, and has a significant impact on the hardening parameters. Furthermore, the initial value of the plastic strain trajectory is seen to be nonzero, and dependent on the test conditions, implying that a change in temperature will give rise to the thermomechanical issues detected with the HiSS function. For a material that is at zero strain rate initially, with a certain nonzero plastic strain, initiation of a test at a given strain rate also changes the value of the plastic strain trajectory inducing spurious plastic strains or else, leads to discontinuous yield. If the initial state before commencement of the test is modeled, the behavior at the start of the test would depend on whether the plastic strain trajectory at the specific strain rate is greater or less than the value at zero strain rate.

Backpredictions

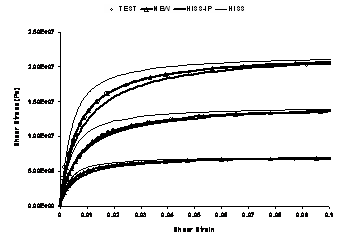
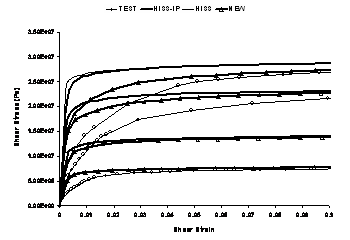
Elastoplastic backpredictions for HiSS, both with and without the iterative parameter determination procedure, marked here HISS-IP and HISS respectively, implicitly assume that the sample was created at the test temperature, as otherwise temperature changes while cooling from the melting point of solder to the storage temperature, and finally, to the test temperature would create spurious hardening and corresponding plastic strain increments in the material over and above the initial plastic strain trajectory. The new function, marked as NEW, does not suffer from these issues. The three strain-rate curves available at any temperature are plotted on the same plot.

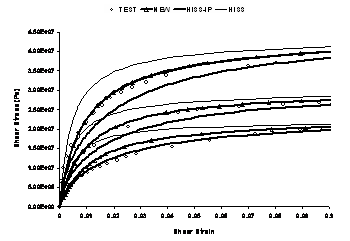
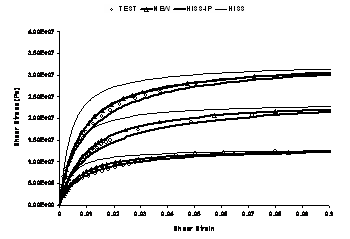
Temperature = -20^oC

Temperature = 25^oC

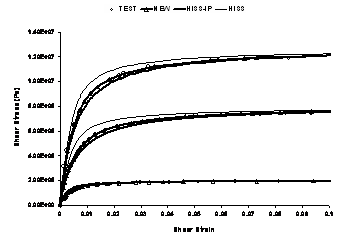
Temperature = 75^oC

Temperature = 125^oC

Both NEW, with zero initial plastic strain trajectory, and HISS-IP with internally consistent hardening parameters developed here, provide better backpredictions than HISS, even for the case of shear even though issues with HiSS are expected to be related primarily to thermal cycling, discussed subsequent to the Perzyna scheme, which are extremely significant for solder as most field loading is thermomechanical.

Perzyna Viscoplastic Scheme

The Perzyna elastoviscoplastic scheme, developed originally to simulate delayed plasticity under high strain rates, assumes all inelastic strain to be viscoplastic and the stress‑strain relationship to be

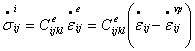
Thermal strains for non‑isothermal loading, and the effect of temperature‑dependence of material parameters may need to be incorporated in Eq. (4) as for the elastoplastic case. The viscoplastic strain rate is given by

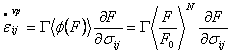
where G is the fluidity parameter, F is the static yield function in terms of the elastoplastic parameters in the limit of zero strain rate, represented by a function such as the new yield function or HiSS, F₀ is a reference value of F used for non-dimensionalizing the flow function f,  and N is a material parameter. The scheme has been applied by Chia (1994),  Desai et al. (1997) and Wang (2001) to simulate creep in solder.

Parameter Determination

Elastic parameters at any temperature are obtained from the highest strain-rate test curve available at that temperature. Plasticity parameters for the static yield surface are obtained from the lowest strain-rate curve available, in conjunction with the elastic modulus obtained from the highest rate curve. Details are in Dube (2004). As seen for the elastoplastic case, the parameter R reported by Wang et al. (2001) requires correction.

To obtain viscous parameters G and N at any temperature without averaging curve-fitted parameters for individual tests, the governing equation under constant strain rate, at the steady-state asymptotic conditions of constant ultimate stress, is rearranged to (Dube, 2004)

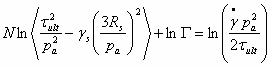
and the best-fit line is obtained using the two strain rates higher than the static yield surface. The equation demonstrates that if R is too high, as is the case for Wang et al. (2001), the coefficient of N on the left hand side cannot be computed. The parameter G computed here is several orders of magnitude smaller than the values presented in Desai et al. (1997), obtained from Chia (1994), where at each loading step, F = 0 was used to compute a and the value of F at the next step was computed based on the a thus computed. Under the Perzyna scheme, F = 0 at any step implies that the viscoplastic strain‑rate is zero. The steady‑state asymptote for constant strain‑rate tests is towards constant stress, i.e. nonzero viscoplastic strain‑rate equal to the applied rate and thus, a corresponding nonzero F.

Solder Parameters for Elastoplastic Scheme

n = 0.4; g = 0.00112; b = 0; n (HiSS) = 2.15 (Wang et al., 2001); n (new function) = 2

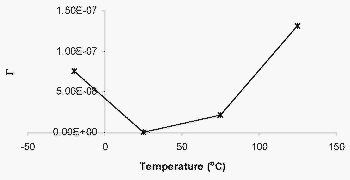
As predicted, the fluidity parameter for the Perzyna elastoviscoplastic simulation shows anomalous behavior at low temperatures, with the value at -20^oC being higher than that at 75^oC, indicating the formulation may not be suitable at low temperatures. The parameter N is relatively constant, in line with general observations (Perzyna, 1966).

Backpredictions

Perzyna viscoplastic backpredictions are carried out at the two higher strain rate test curves available. NEW provides somewhat better simulations than HISS and HISS-IP, which are essentially identical.

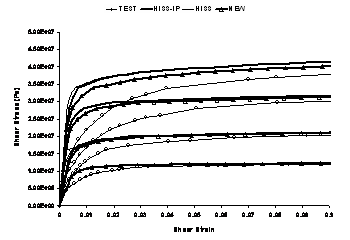
Strain-Rate = 2.78 x 10^-2/s

Strain-Rate = 2.78 x 10^-3/s

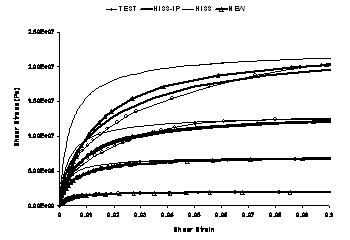
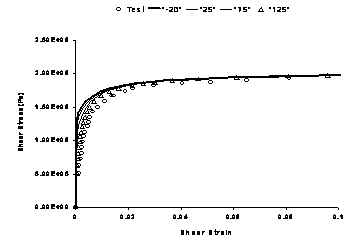
The slowest strain rate curve is the static yield surface, and as shown, elastoplastic backpredictions for the same provide excellent results. Thus, whether the elastic modulus for this surface is obtained as the slope of the highest strain-rate curve or from the lowest strain-rate curve, a corresponding set of plasticity parameters can be determined and both sets will provide reasonable backpredictions. NEW and HISS-IP continue to provide improved simulations for elastoplastic behavior.

Strain-Rate = 2.78 x 10^-4/s Static Surfaces

Yield Function Issues

Thermal concerns associated with HiSS are crucial for package simulations, as loading is often driven by the thermal mismatch in thermomechanical problems. The large variation of x₀ with temperature for the improved HiSS parameters implies that while the internally consistent parameters provide improved backpredictions, they also provide large spurious plastic strains.

For low‑strain rates typical for field conditions, Perzyna backpredictions approach the static yield surfaces with parameters and from the x₀ values for the elastoviscoplastic parameters, for cooling from 125^oC to -20^oC, the improved HiSS parameters provide a linear plastic strain increment of approximately 2.0% in addition to the thermal contraction, while assuming the CTE of solder over the range to be 26 x 10^-6, the thermal contraction for the same temperature change is 0.38%. The spurious plastic strains are substantially larger than the thermal contraction. Similar results are observed for the elastoplastic scheme. For the new function, the strain is only due to thermal expansion and contraction, as is expected for metals.

Total Strain upon Cooling from 125^oC vs. Final Temperature

While at 125^oC, HiSS results such as for the static yield surface are identical to the new function, samples are created at the melting point of solder and are then stored at a cooler temperature, typically room temperature. Including the pre‑test thermal loading in simulations leads to spurious thermal‑history dependence for HiSS The yield stress at 125^oC, as a function of the ‘storage’ temperature for the HiSS function based on the improved and the original parameters. For comparison, the ultimate stress that can be assumed to be achieved during the static-surface test, sans degradation, is included (marked as Assumed ULTIMATE). The yield stress for HiSS is seen to be a significant proportion of the peak stress attained in the test, while the new yield function maintains a yield stress of zero and provides continuous yield.

Yield Stress at 125^oC vs. Prior Cooling Temperature

Stress‑strain backpredictions for the HiSS based on original parameters and the improved parameters at 125^oC, taking into account the yield stress due to prior cooling to lower temperatures show a spurious dependence on thermal history not shown by the the new yield function.

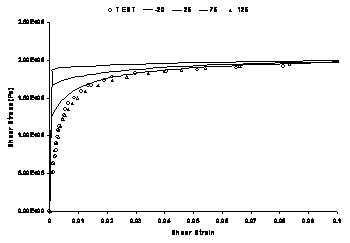
HISS

HISS-IP

Degradation Modeling

Degradation modeling in terms of DSC was used for both the elastoplastic and the viscoplastic simulations. For elastoplastic simulations, disturbance was modeled in terms of the standard version based on the deviatoric plastic strain trajectory as well as two approximate formulations (Dube, 2004) based on dissipated work, one where the dissipated work in the RI material is used to compute disturbance, and another where the work dissipated in the observed material is used instead.

Disturbance Parameters for Elastoplastic Simulation

As can be seen, the parameter obtained based on dissipated work are extremely cumbersome to work with, and do not show less variation with loading conditions such as temperature or strain rate than those for the deviatoric plastic strain trajectory. Furthermore results show no improvements in backpredictions, as shown by a typical results plot for the new yield function.

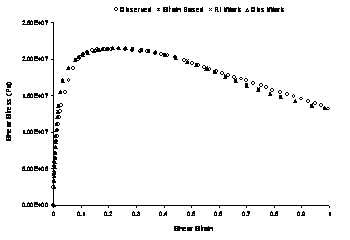
Disturbance Parameters for Viscoplastic Formulation

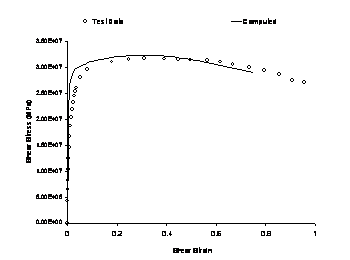
As shown by the results, reasonable results are obtained for the backpredicted observed curve based on both the viscoplastic computation as well as the elastoplastic computations, and it is difficult to distinguish between models based on the test data itself. In fact, results are better for the rate-dependent elastoplastic formulation which, under general load conditions is not applicable. However, direct application of Finite Elements may not be helpful due to the complexity of the schemes, including cases such as use of incomplete formulations, and thus, it is essential to conduct analyses based on simple loading conditions to the greatest extent feasible. Such analyses predicted potential problems with the elastoplastic analysis under general loading conditions, in view of the correct incremental formulation, as well as potential issues with the Perzyna formulation at lower temperatures even before the validations based on the test data were conducted.