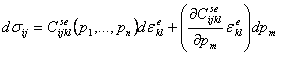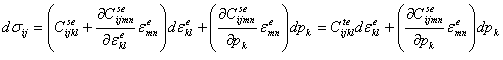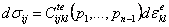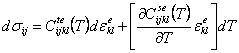Elastic Deformations

Elastic strains are instantaneous deformations, which are fully recovered when the applied load is removed. The stress-strain relationship is history independent, expressible at any instant, t, as

where (s)_t, the stress tensor at time t, is some function, F, of the instantaneous values of the elastic strain tensor e^e and the n additional parameters p_i that may be relevant to the elastic response. For instance, the stress required to induce a given elastic strain typically depends on the temperature.

Since many materials are linear elastic, it is convenient to write the relationship as

where C_ijkl^se is the secant elastic constitutive matrix which may depend on the instantaneous values of the n parameters, p₁,…,p_n, and e^e_kl is the elastic strain tensor. If the material elastic response is nonlinear, the secant matrix itself depends on the elastic strain, which is then one of the n parameters.

Incremental Elastic Equation

The incremental stress-strain relationship for elastic deformations, where the summation notation is extended to the index for the parameters p_m, m varying from 1 to n, is then

If the stress-strain relationship is nonlinear, the elastic strain dependence of the secant matrix can be incorporated in terms of the tangent constitutive matrix C_ijkl^te and the remaining n-1 parameters p_k as

Note the difference from the equation used in some prior work,

which does not include the effect of dependence of the secant elastic matrix on parameters such as temperature.

Implications of Generalized Incremental Elastic Equation

For a material with only temperature-dependent elastic parameters, the incremental equation is

The significance of the temperature-induced stress increment depends on the problem, and cases can be contrived in which only the correction term is nonzero. Thus it cannot be assumed to be negligible a priori. The basic elastic stress-strain incremental relationship is also assumed to hold for, and thus impacts, the incremental elastoplastic formulation. Significant implications arise for complex materials, where simplifications have been used, such as for solder, where strain-rate dependent parameters have been used under an elastoplastic formulation to approximate creep, or for geotechnical materials, where the elastic parameters may be assumed to depend on the mean pressure.

Comparison of Prior and Generalized Incremental Formulations

Click on slide buttons to navigate slideshow

The generalized incremental formulation still does not incorporate the thermoelastic effect, whereby mechanical deformations and heat transfer are interlinked. A new thermomechanical model (Dube, 2004) is proposed in terms of unified stress-strain-temperature relationships. The material response inherently incorporates the thermoelastic effect, with the governing equations intrinsically capable of predicting the variation of elastic parameters and the coefficient of thermal expansion with temperature based on their basic definitions. Examples are presented for Aluminum, Lead, Tin and Solder.