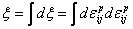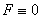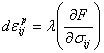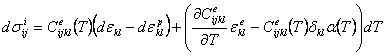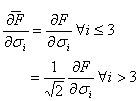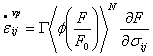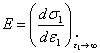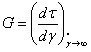|
Plastic Deformations
Plastic deformation is irreversible and typically considered instantaneous. The material does not regain its original shape upon unloading. Plastic deformation may often be negligible at low stresses, with an abrupt increase above a specific stress level termed the yield stress for the material. However for several materials the yield stress in not well defined and continuous yielding starting at the state of zero stress must be modeled.
A perfectly plastic material is one that cannot withstand any stress increase over the yield stress, and undergoes unlimited plastic deformation at the yield stress. For most materials, once plastic yielding commences, the stress required for further plastic deformation increases with plastic strain and the material is said to undergo hardening. If the material is unloaded and then reloaded, the state of stress at which yielding commences depends on the prior hardening.
The theory of plasticity assumes that there exists a yield function F, which provides the required combination of the state of stress and the hardening, h, in the material for continuing yield (Hill, 1950),
Plastic Strain Trajectory For modeling purposes, hardening may be expressed as a function of the history of the plastic strain increments, or the associated work dissipated. For multiaxial stress states and corresponding strain increments, an appropriate scalar function for the history of plastic strain increments can be taken to be the plastic strain trajectory defined as (e.g. Desai, 2001)
It may be noted that an alternate definition of plastic strain trajectory in terms of the engineering plastic strain vector (Desai, 2001; Wang et al., 2001)
where eip denote components of the engineering plastic strain vector should be avoided. It is numerically different from the tensor definition and inconsistent results would be obtained if the two definitions were to be used interchangeably for modeling. More importantly, the plastic strain trajectory defined using engineering strains is not an invariant and simulation results would demonstrate spurious dependence on the coordinate axes chosen for the problem.
The yield function then is
Consistency Condition The equation
defines a surface in stress-space, for a given value of the hardening, which separates the region of elastic and elastoplastic deformation. The surface must be a convex surface in stress space. In the interior of the surface, the function F is negative and deformation is elastic. On the surface, F is zero and stress increments directed towards the inside lead to elastic unloading while stress increments along the surface lead to elastic neutral loading. Plastic deformations occur for stress increments directed outwards, which would make F positive if the hardening were to remain unchanged. This is accompanied by a corresponding increase in hardening, and the yield surface expands simultaneously in a manner that it always passes through the state of the applied stress at that instant. An important consequence of this approach is that for any possible combination of the state of stress and hardening which is possible for a material, the material can never be outside of the yield surface.
The combination of loading and hardening in the material can always be assumed to satisfy the condition that F remains zero and the material remains on the yield surface. This constraint, termed the consistency condition, is
Typically, the yield stress, and thus, material parameters describing yield are functions of temperature. More generally, as for the elastic constitutive matrix, the yield function may depend on n additional parameters hi (e.g. Cook, 1988), such as temperature and strain rate , whereby it can be written as
The consistency condition then becomes
This by itself is insufficient to provide the plastic strain increment for a given stress increment as increments of the function x do not define all components of the plastic strain increment uniquely, and another condition for individual components of the incremental plastic strain tensor is required.
Normality Rule For associated plasticity, the plastic strain increments are computed based on the normality assumption
where l is a scalar and F is the yield function.
Incremental Elastoplastic Equation
Assuming that the total strain is given by the sum of the elastic (e), plastic (p) and thermal (T) strains,
where thermal strains are due to the coefficient of linear expansion, the incremental stress‑strain relationship for temperature‑dependent elastic parameters can be written as
In conjunction with the consistency condition for the temperature dependent case
and the normality rule following Wang (2001), this provides the generic equation for a material with temperature-dependent elastic and plasticity parameters can be derived to be
where
The essential difference between the equation of Wang (2001) and this equation is the presence of additional terms in the incremental elastic stress-strain equation, which provide the increment in stress due to the change in elastic parameters with temperature. As part of the thermomechanical model, a yield equation with temperature-independent plasticity parameters is developed for metals.
The incremental equation incorporates the effect of change in elastic parameters with temperature on the elastoplastic formulation. However, if material parameters are treated as strain-rate dependent, the formulation becomes overly complex while being potentially inaccurate if the strain-rate dependence is used only to simplify creep modeling, which for instance is the case for, rate‑dependent elastoplastic formulation for solder.
The interpretation of the term instantaneous for plastic strains depends to a large extent on the time scale involved. At extremely high strain rates, plastic yield may indeed depend on strain rate, with delayed yielding and delayed plastic deformations. For such cases, a more appropriate approach is to treat plastic strains as time-dependent viscoplastic strains (Perzyna, 1966).
The Perzyna (1966) formulation was developed based on observations regarding the delayed yielding and time-dependence of post-yield material response under relatively high strain-rate loading, such as for wave propagation and impact loading problems, with strain rates up to 104/s. The formulation assumes all irreversible strain in the material to be viscoplastic, and thus
where
where F is the plastic yield function in terms of material parameters determined from the “static” yield surface, which governs the material behavior at vanishingly small strain rates. At high strain rates the material behavior becomes increasingly elastic, and as the strain rate tends to infinity the initial material behavior is purely elastic and elastic parameters are obtained as
The Perzyna formulation is not intended to model time-dependent post-yield viscous plastic strains as well as creep strains simultaneously. At extremely high strain rates, where plastic yield is delayed, creep strains do not have sufficient time to manifest. The Perzyna formulation has been used to model solder (e.g. Chia, 1994; Desai and Whitenack, 2001; Wang et al., 2001), but a significant correction to the procedure for parameter determination (Dube, 2004) confirms that problems arise in regimes where both plastic yielding and creep are present in terms of anomalous behavior of parameters.
Both the elastoplastic scheme and the Perzyna viscoplastic scheme require specification of the yield function, F. Several yield functions have been developed over the years, for applications to various materials, including the new yield function developed here. Additionally, as part of the thermomechanical model for metals, a yield criterion is developed in terms of temperature-independent parameters, which is compatible with the observed relationship between dislocation density and hardening.
|