Creep Deformation

Creep deformation relates to irreversible deformation that is manifest over time, and is typically significant above temperatures which are greater than half the melting point on the absolute scale. Creep strains can be divided into three regions, an initial high strain rate primary component, followed by a lower rate steady-state secondary component and finally, a tertiary phase with an increasing strain rate leading to failure. Dowling (1993) quotes Andrade’s results for creep for metals in general to indicate that creep curves at constant true stress might not show tertiary creep. In certain cases, secondary creep may be suppressed and the steady-state creep rate is replaced by the minimum creep rate (Cadek, 1988).

Primary and secondary regions of creep are typically expressed as functions of stress, time and temperature, in terms of separable functions (Ju et al., 1994) in the form

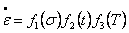
where suggested forms for the stress-dependence for secondary creep include

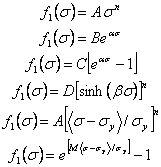
For time-dependence of primary creep, functions used include

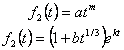
 Temperature dependence is usually in the form of Arrhenius type relationships

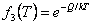
Examples of equations for steady-state creep include the Dorn equation (Guo et al., 1992)

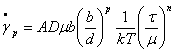
where

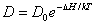
with g_p being the inelastic shear strain, D the appropriate diffusion coefficient, m the shear modulus, b the Burgers vector, t the applied shear stress, d the grain size or interphase spacing, A, n, p being material constants. D₀ is a constant and DH is the activation energy for a specific diffusion mechanism, while k is the Boltzmann constant.  Similar equations including a back stress may be used, such as

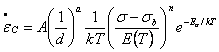
Several deformation mechanisms may contribute to creep. Dislocation glide may be significant at lower temperatures and higher stresses. At high temperatures and relatively low stresses, vacancy diffusion may be dominant, either through grain boundaries as Coble creep, or at higher temperatures, through the crystal as in Nabarro-Herring creep. Both grain boundary and matrix creep may be represented by a Weertman-type equation of the form

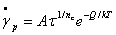
where the constants A and n_c depend on the dominant creep mechanism and Q is the relevant energy of activation.

In certain cases, creep may dominate to an extent that plastic strains are negligible, and the Perzyna (1966) viscoplastic model, originally developed for time-dependent behavior manifested above yield stress, may be used to simulate creep with the static surface being the stress level below which creep is negligible. However, it must be noticed that if both plastic yield and creep are present and are comparable in significance, the creep behavior will be observed below the yield surface and the plastic yield surface for plastic deformations cannot be used as the static yield surface and inconsistent parameters may result as seen for the fluidity parameter of solder. In such cases, two yield surfaces are required, one for plastic yield which is treated as instantaneous, and a static yield surface for creep, which is attained in tests which are conducted in the limit of zero strain rate.

In the Perzyna formulation, the total strain rate at any time is assumed to be the sum of the elastic and the viscoplastic strain rates

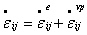
The corresponding rate of stress increment is

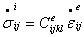
The viscoplastic strain rate is given by

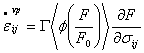
where G is the fluidity parameter, F is the static yield function, F₀ is a reference value of F or any constant so as to render dimensionless, and f is flow function, expressible in several different forms such as (Desai, 2001)

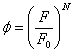
or

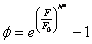
where N and N* are material parameters.

Finally, a preliminary empirical equation is developed as part of the thermomechanical model, for solder. It provides reasonable backpredictions for eutectic lead-tin solder in terms of three temperature-independent parameters, for the test data of Wang et al. (2001) which spans a temperature range of -25^oC to 125^oC and strain rates between 2.28 x 10^-4/s to 2.78 x 10^-2/s.